Superposition Theorem
Superposition Theorem state that in any linear bilateral network having more than one source, the response in any one of the element is equal to algebraic sum of the response caused by individual source while rest of the sources are replaced by their internal resistances.
1.We consider one independent source at a time while all other independent sources are turned off. This implies that we replace voltage source by short circuit and current source by open circuit. This way we obtain a simpler and more manageable circuit.
2.Turn off all independent sources except one source. Find the output (voltage or current) due to that active source.
3.Repeat the above step for each of the other independent sources.
4.Find the total contribution by adding algebraically all the contributions due to the independent sources.
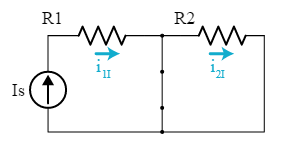
Consider the following linear circuit with two sources: one current source and one voltage source. The two sources are the inputs to the function. For this problem we happen to want to find two outputs, currents i1i, start subscript, 1, end subscript and i2i, start subscript, 2, end subscript.
Let’s analyze this circuit using superposition.
First, we suppress the current source and analyze the circuit with just the voltage source acting alone. To suppress the current source, we replace it with an open circuit.
With just the voltage source, the two output currents are:
i1V=0i2V=R2Vsi, start subscript, 1, V, end subscript, equals, 0, i, start subscript, 2, V, end subscript, equals, start fraction, start text, V, s, end text, divided by, start text, R, end text, 2, end fraction Where
i1Vi, start subscript, 1, V, end subscript and
i2Vi, start subscript, 2, V, end subscript are the currents in
R1start text, R, end text, 1 and
R2start text, R, end text, 2 caused by the voltage source.
Next, we restore the current source and suppress the voltage source, to calculate the contribution of the current source acting alone.
With just the current source, the two output currents are:
i1I=Isi2I=0 Where
i1Ii, start subscript, 1, I, end subscript and
i2Ii, start subscript, 2, I, end subscript are the currents in
R1start text, R, end text, 1 and
R2start text, R, end text, 2 caused by the current source.
We complete the analysis by adding the contributions from each source:
i1=i1V+i1I=0+Is=Isi, start subscript, 1, end subscript, equals, i, start subscript, 1, V, end subscript, plus, i, start subscript, 1, I, end subscript, equals, 0, plus, start text, I, s, end text, equals, start text, I, s, end text i2=i2V+i2I=R2Vs+0=R2
Vs