Kirchhoffs First Law – The Current Law, (KCL)
Kirchhoffs Current Law or KCL, states that the “tthe algebraic sum of flowing currents through a point (or junction) in a network is Zero (0) or in any electrical network, the algebraic sum of the currents meeting at a point (or junction) is Zero (0)“. I(exiting) + I(entering) = 0. This idea by Kirchhoff is commonly known as the Conservation of Charge.
Kirchhoffs Current Law

Here, the three currents entering the node, I1, I2, I3 are all positive in value and the two currents leaving the node, I4 and I5 are negative in value. Then this means we can also rewrite the equation as;
I1 + I2 + I3 – I4 – I5 = 0
The term Node in an electrical circuit generally refers to a connection or junction of two or more current carrying paths or elements such as cables and components. Also for current to flow either in or out of a node a closed circuit path must exist. We can use Kirchhoff’s current law when analysing parallel circuits.
Kirchhoffs Second Law – The Voltage Law, (KVL)
Kirchhoffs Voltage Law or KVL, states that “in any closed loop network, the total voltage rise in the loop is equal to the sum of all the voltage drops within the same loop”. In other words the algebraic sum of all voltages within the loop must be equal to zero. This idea by Kirchhoff is known as the Conservation of Energy.
Kirchhoffs Voltage Law

Starting at any point in the loop continue in the same direction noting the direction of all the voltage drops, either positive or negative, and returning back to the same starting point. It is important to maintain the same direction either clockwise or anti-clockwise or the final voltage sum will not be equal to zero. We can use Kirchhoff’s voltage law when analysing series circuits.
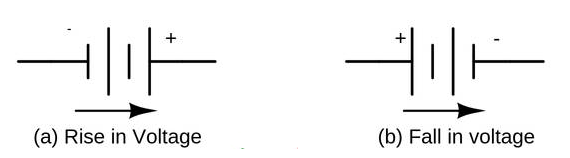


No comments:
Post a Comment